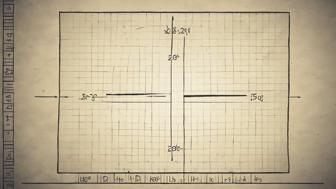
Um den Umfang eines Rechtecks zu berechnen, sind die Länge und die Breite erforderlich. Die Formel dafür lautet: Umfang = 2 × (Länge + Breite). Hierbei ist die Länge die längere Seite des Rechtecks, während die Breite die kürzere Seite darstellt. Um den Umfang in der jeweiligen Maßeinheit auszudrücken, addiert man die beiden Seiten und multipliziert die Summe mit zwei. Der Umfang kann auch zur Flächenberechnung genutzt werden, auch wenn Flächeninhalt und Diagonalenlänge unterschiedliche Maße haben. Für eine schnellere Berechnung kann ein Online-Rechner verwendet werden. Zudem ist der Umkreisradius eines Rechtecks von großer Bedeutung, da er häufig für geometrische Analysen und grafische Darstellungen benötigt wird. Die Genauigkeit der verwendeten Maße beeinflusst entscheidend die Präzision der Umfangsberechnung.
Formeln für verschiedene geometrische Formen
Die Berechnung des Umfangs ist für verschiedene geometrische Formen essenziell. Jede Form hat ihre spezifische Formel, um den Umfang korrekt zu ermitteln. Für ein Rechteck wird der Umfang durch die Formel U = 2 * (Länge + Breite) berechnet, wobei die Seitenlängen in die Berechnung einfließen. Bei einem Quadrat, dessen Seiten gleich lang sind, vereinfacht sich die Formel zu U = 4 * Seite.
Für ein Dreieck lautet die Umfangsformel U = a + b + c, wobei a, b und c die Längen der Seiten sind. Der Umfang eines Kreises hingegen lässt sich mit der Formel U = 2 * π * r, wobei r der Radius ist, angeben. Bei einem Trapez benötigen wir die Längen der parallelen Seiten sowie der beiden anderen Seiten: U = a + b + c + d.
Das Parallelogramm verwendet die Formel U = 2 * (Basis + Höhe). Ein Drachenviereck oder eine Raute, beides mit gleich langen Seiten, wird wie ein Quadrat behandelt: U = 4 * Seite. Diese Beispiele verdeutlichen, wie vielfältig die Berechnung des Umfangs geometrischer Formen ist.
Kreisumfang: Radius und Durchmesser
Der Umfang eines Kreises lässt sich durch die sogenannte Kreisformel berechnen, die auf dem Radius und dem Durchmesser basiert. Die Formel lautet: Umfang = 2 * Pi * Radius oder alternativ Umfang = Pi * Durchmesser. Hierbei ist Pi eine mathematische Konstante, deren Wert ungefähr 3,14 beträgt, wobei weitere Nachkommastellen für präzisere Berechnungen verwendet werden können. Neben dem Umfang spielt auch der Flächeninhalt eine wesentliche Rolle, der mit der Formel Fläche = Pi * Radius² berechnet wird. Die Herleitung dieser Formeln beruht auf den geometrischen Eigenschaften der Kreisform. Bei der Berechnung des Umfangs eines Kreises sind die Ergebnisse direkt von der Auswahl des Radius oder des Durchmessers abhängig, wodurch beide Größen eng miteinander verknüpft sind. Verständnis der Zusammenhänge zwischen diesen Begriffsdefinitionen und den entsprechenden Formeln ist entscheidend für präzise geometrische Berechnungen.
Beispiele zur Umfangsberechnung
Umfangsberechnungen sind für viele geometrische Formen entscheidend, um ihre Eigenschaften zu verstehen. Für ein Quadrat besteht die Formel zur Umfangsberechnung darin, die Länge einer Seite mit 4 zu multiplizieren. Bei einem Rechteck hingegen lautet die Formel: Umfang = 2 × (Länge + Breite). Für ein Dreieck berechnet man den Umfang, indem man die Längen aller drei Seiten addiert. Der Umfang eines Kreises wird durch die Formel 2 × π × Radius bestimmt, wobei π etwa 3,14 ist. Für ein Trapez addiert man die Längen der beiden parallelen und der beiden nicht parallelen Seiten. Ein Parallelogramm nutzt auch die Formel für das Rechteck, doch die Seitenlängen müssen dabei unterscheiden. Bei speziellen Formen wie der Raute oder dem Drachenviereck addiert man ebenfalls die Seitenlängen. Diese Beispiele zeigen, wie vielseitig die Berechnung des Umfangs in der Geometrie ist.